Chapter 10 Global Spatial Autocorrelation 1

Introduction

This notebook cover the functionality of the Global Spatial Autocorrelation 1 section of the GeoDa workbook. We refer to that document for details on the methodology, references, etc. The goal of these notes is to approximate as closely as possible the operations carried out using GeoDa by means of a range of R packages.

The notes are written with R beginners in mind, more seasoned R users can probably skip most of the comments on data structures and other R particulars. Also, as always in R, there are typically several ways to achieve a specific objective, so what is shown here is just one way that works, but there often are others (that may even be more elegant, work faster, or scale better).

For this notebook, we use Cleveland house price data. Our goal in this lab is show how to assign spatial weights based on different distance functions.

10.0.1 Objectives

After completing the notebook, you should know how to carry out the following tasks:

Visualize Moran’s I with a Moran scatterplot
Carry out inference using the permutation approach
Make analysis reproducible with the random seed
Create a LOWESS smooth of the Moran scatter plot
Conduct a Chow test with the Moran scatterplot
Analyze the range of spatial autocorrelation by means of a spatial correlogram

10.0.1.1 R Packages used

sf: To read in the shapefile and make queen contiguity weights
spdep: To create k-nearest neighbors and distance-band neighbors, calculate distances between neighbors, convert to a weights structure, and coercion methods to sparse matrices.
ggplot2: To make customized plots such as a Moran’s I scatter plot and spatial correlogram.
Hmisc: To get LOWESS smoother functionality in ggplot2.
robustHD: To compute standarized scores for variables and lag variables. in construction of a Moran’s I scatterplot
deldir: To create voronoi polygons.
tidyverse: For basic data frame manipulation.
gap: To compute chow test statistics.
gridExtra: To pack multiple plots into one, mainly used to construct the spatial correlogram
geodaData: To access the data for this tutorial

10.0.1.2 R Commands used

Below follows a list of the commands used in this notebook. For further details and a comprehensive list of options, please consult the R documentation.

Base R: install.packages, library, setwd, rep, sd, mean, summary, attributes, lapply, class, length, which, data.frame, plot
sf: st_read, st_relate, st_as_sf
spdep: dnearneigh, nb2listw, sp.correlogram, Szero
ggplot2: ggplot, geom_smooth, geom_point, xlim, ylim, geom_hline, geom_vline, geom_line, ggtitle, scale_x_continous
Hmisc: stat_plsmo
robustHD: standardized
deldir: deldir
tidyverse: filter
gap: chow.test
gridExtra: grid.arrange

10.1 Preliminaries

Before starting, make sure to have the latest version of R and of packages that are compiled for the matching version of R (this document was created using R 3.5.1 of 2018-07-02). Also, optionally, set a working directory, even though we will not actually be saving any files.²⁷

10.1.1 Load packages

First, we load all the required packages using the library command. If you don’t have some of these in your system, make sure to install them first as well as their dependencies.²⁸ You will get an error message if something is missing. If needed, just install the missing piece and everything will work after that.

library(sf)
library(spdep)
library(ggplot2)
library(deldir)
library(robustHD)
library(Hmisc)
library(tidyverse)
library(gap)
library(gridExtra)
library(geodaData)

geodaData website

All of the data for the R notebooks is available in the geodaData package. We loaded the library earlier, now to access the individual data sets, we use the double colon notation. This works similar to to accessing a variable with $, in that a drop down menu will appear with a list of the datasets included in the package. For this notebook, we use clev_pts.

Otherwise, to get the data for this notebook, you will and to go to Cleveland Home Sales The download format is a zipfile, so you will need to unzip it by double clicking on the file in your file finder. From there move the resulting folder titled: nyc into your working directory to continue. Once that is done, you can use the sf function: st_read() to read the shapefile into your R environment.

clev.points <- geodaData::clev_pts

10.1.2 Making the weights

The weights used for this notebook are queen contiguity, based off voronoi polygons contructed from the point data for this notebook. In order to make the weights, we must first construct voronoi polygons from the cleveland point data. There are a number of ways to do this. We will be using the deldir package as a starting point. We will need to convert the result from the deldir package to class sf, which we have been working with throughout the notebooks.

The only function we need from deldir is deldir, which outputs a data structure with voronoi polygons. The only inputs needed are a vector of the x coordinates and a vector of the y coordinates. The base R plot function can give us a preliminary look at the voronoi polygons. We will need a few additional parameters other than vtess, so the plot is legitable. Set wlines = "tess", wpoints = "none" and lty = 1.

vtess <- deldir(clev.points$x, clev.points$y)
plot(vtess, wlines="tess", wpoints="none",
      lty=1)

This function will be used to convert the deldir voronoi polygons to sp, where we can easily convert them to sf. We are not going to cover the individual steps of this function because it is outside the scope of these notebooks. The important thing to note here is that this function converts deldir voronoi polygons to sp.

voronoipolygons = function(thiess) {
w = tile.list(thiess)
polys = vector(mode='list', length=length(w))
for (i in seq(along=polys)) {
    pcrds = cbind(w[[i]]$x, w[[i]]$y)
    pcrds = rbind(pcrds, pcrds[1,])
    polys[[i]] = Polygons(list(Polygon(pcrds)), ID=as.character(i))
}
SP = SpatialPolygons(polys)
 voronoi = SpatialPolygonsDataFrame(SP, data=data.frame(dummy = seq(length(SP)), row.names=sapply(slot(SP, 'polygons'), 
    function(x) slot(x, 'ID'))))
}

Again, we can use the base R plot function to take a look at voronoi polygons. Now that they are class sp, we don’t need the extra parameters in plot.

v <- voronoipolygons(vtess)
plot(v)

With the voronoi polygons in sp class, we can easily conert them to sf with st_as_sf. Again we use the base R plot function to view the polygons.

vtess.sf <- st_as_sf(v)
plot(vtess.sf$geometry)

Now that we have the voronoi polygons as an sf object, we can use the queen contiguity process outline in the Contiguity Based Weights notebook. We will briefly cover each step of the process. For more indepth information please see the Contiguity Based Weights notebook.

To start we create a function for queen contiguity, which is just st_relate with the specified pattern for queen contiguity which is F***T****

st_queen <- function(a, b = a) st_relate(a, b, pattern = "F***T****")

We apply the queen contiguity function to the voronoi polygons and see that the class of the output is sgbp. This structure is close to the nb structure, but has a few differences that we will need to correct to use the rest of spdep functionality.

queen.sgbp <- st_queen(vtess.sf)
class(queen.sgbp)

## [1] "sgbp" "list"

This function converts type sgbp to nb. It is covered in more depth in the Contiguity Based Weight notebook. In short, it explicitly changes the name of the class and deals with the observations that have no neighbors.

as.nb.sgbp <- function(x, ...) {
  attrs <- attributes(x)
  x <- lapply(x, function(i) { if(length(i) == 0L) 0L else i } )
  attributes(x) <- attrs
  class(x) <- "nb"
  x
}

We use as.nb.sgbp to convert neighbor types and then check the class with class.

queen.nb <- as.nb.sgbp(queen.sgbp)
class(queen.nb)

## [1] "nb"

To go from neighbors object to weights object, we use nb2listw, with default parameters, we will get row standardized weights.

queen.weights <- nb2listw(queen.nb)

10.2 The Moran Scatter Plot

10.2.1 Concept

10.2.1.1 Moran’s I

Moran’s I statistic is arguably the most commonly used indicator of global spatial autocorrelation. It was initially suggested by Moran (1948), and popularized through the classic work on spatial autocorrelation by Cliff and Ord (1973). In essence, it is a cross-product statistic between a variable and its spatial lag, with the variable expressed in deviations from its mean. For an observation at location i, this is expressed as $z_i = x_i - \bar{x}$, where $\bar{x}$is the mean of variable x.

Moran’s I statistic is then:

\[I = \frac{\Sigma_i\Sigma_jw_{ij}z_iz_j/S_0}{\Sigma_iz_i^2/n}\] with $w_{ij}$ as elements of the spatial weights matrix, $S_0 = \Sigma_i\Sigma_jw_{ij}$ as the sum of all of the weights and n as the number of observations.

10.2.1.2 Permutation inference

Inference for Moran’s I is based on a null hypothesis of spatial randomness. The distribution of the statistic under the null can be derived using either an assumption of normality (independent normal random variates), or so-called randomization (i.e., each value is equally likely to occur at any location).

An alternative to an analytical derivation is a computational approach based on permutation. This calculates a reference distribution for the statistic under the null hypothesis of spatial randomness by randomly permuting the observed values over the locations. The statistic is computed for each of these randomly reshuffled data sets, which yields a reference distribution.

This distribution is then used to calculate a so-called pseudo p-value. This is found as \[p = \frac{R +1}{M+1}\] where R is the number of times the computed Moran’s I from the spatial random data sets (the permuted data sets) is equal to or more extreme than the observed statistic. M equals the number of permutations. The latter is typically taken as 99, 999, etc., to yield nicely rounded pseudo p-values.

The pseudo p-value is only a summary of the results from the reference distribution and should not be interpreted as an analytical p-value. Most importantly, it should be kept in mind that the extent of significance is determined in part by the number of random pemutations. More precisely, a result that has a p-value of 0.01 with 99 permutations is not necessarily more significant than a result with a p-value of 0.001 with 999 permutations.

10.2.1.3 Moran scatter plot

The Moran scatter plot, first outlined in Anselin (1996), consists of a plot with the spatially lagged variable on the y-axis and the original variable on the x-axis. The slope of the linear fit to the scatter plot equals Moran’s I.

We consider a variable z, given in deviations from the mean. With row-standardized weights, the sum of all the weights (S0) equals the number of obsevations (n). As a result, the expression for Moran’s I simplifies to:

\[I= \frac{\Sigma_i\Sigma_jw_{ij}z_iz_j}{\Sigma_iz_i^2} = \frac{\Sigma_i(z_i*\Sigma_jw_{ij}z_j)}{\Sigma_iz_i^2}\]

Upon closer examination, this turns out to be the slope of a regression of $\Sigma_jw_{ij}z_i$ on $z_i$ This is the principle underlying the Moran scatter plot.

An important aspect of the visualization in the Moran scatter plot is the classification of the nature of spatial autocorrelation into four categories. Since the plot is centered on the mean (of zero), all points to the right of the mean have $z_i>0$ and all points to the left have $z_i<0$. We refer to these values respectively as high and low, in the limited sense of higher or lower than average. Similarly, we can classify the values for the spatial lag above and below the mean as high and low.

The scatter plot is then easily decomposed into four quadrants. The upper-right quadrant and the lower-left quadrant correspond with positive spatial autocorrelation (similar values at neighboring locations). We refer to them as respectively high-high and low-low spatial autocorrelation. In contrast, the lower-right and upper-left quadrant correspond to negative spatial autocorrelation (dissimilar values at neighboring locations). We refer to them as respectively high-low and low-high spatial autocorrelation.

The classification of the spatial autocorrelation into four types begins to make the connection between global and local spatial autocorrelation. However, it is important to keep in mind that the classification as such does not imply significance. This is further explored in our discussion of local indicators of spatial association (LISA).

10.2.2 Creating a Moran scatter plot

Before we create the Moran’s I scatterplot, we will get the statistic using moran from spdep. For this function, we need the a variable to do the Moran’s I on, a weights structure, the length of the dataset, and then Szero of the queen weights, which calculates the constants needed for tests of spatial autocorrelation.

moran <- moran(clev.points$sale_price, queen.weights, length(queen.nb), Szero(queen.weights))
moran$I

## [1] 0.2810649

We get a value of .281, which is the Moran’s I statistic, which also corresponds to the slope of the Moran’s I scatter plot.

In creating the Moran’s I scatterplot, we will need to to create a lag variable of sale price from our queen weights. This is just done with the function lag.listw, which takes a weights structure and a variable of equal length to create a lag variable from.

clev.points$lagged_sale_price <- lag.listw(queen.weights,clev.points$sale_price)
clev.points$lagged_sale_price

##   [1]  83287.500 112912.500  80178.571 108550.000  58375.000  96816.667
##   [7] 115600.000  41503.571  59732.143  80025.000  48785.714 110750.000
##  [13] 103000.000  72300.000 113050.000 141918.167 112900.000  55142.857
##  [19] 140594.143  88871.429 213734.833 176844.143 201950.000 134800.000
##  [25]  67350.000  46371.375  88125.000 137600.000 107625.000  28357.143
##  [31]  26218.750   9025.000  18291.667  25950.000   7002.667  41863.300
##  [37]  28187.500  17300.000  10250.000  25333.333  18418.750  21437.500
##  [43]  26430.000  20771.000  60539.000  43412.500 102080.375  24936.667
##  [49]  29619.143  28094.200  16657.000  18691.500  22193.625  21575.667
##  [55]  17804.571 128700.000  35710.400  45935.250  36411.500  42500.000
##  [61]  82133.333  71680.000  81100.000  55733.333  69066.667  66600.000
##  [67]  39300.000  59750.000  58000.000  48625.000  45593.750  15441.667
##  [73]  47174.750  33416.667  35150.000  34083.500  51762.500  36304.750
##  [79]  31783.600  12908.000  14676.600  15166.667  22483.333  19541.667
##  [85]  20426.600  21100.000  36212.000  20900.000  32775.000  29946.600
##  [91]  44350.333  24431.286  21279.750  62380.000  21683.667  25914.900
##  [97]  42369.667   8481.000  10904.800  13657.000  13830.000  14412.250
## [103]  24264.143  14487.333  32960.571  12226.800   8708.500  12655.667
## [109]  15714.286  20383.333  21151.667  10258.571  18451.667 131651.500
## [115]  20420.000 182072.714 140650.000  22034.000  43550.000  53100.000
## [121]  41488.889  26500.000  13095.714   8764.444   9208.667   6156.667
## [127]  11761.333   5529.500   7409.600  40510.000  34388.286   9250.000
## [133]   9128.000  15470.000  12699.714  18842.000  14440.000  10125.000
## [139]  17967.500   9500.000  30250.000  17400.000  11174.000  13248.833
## [145]   9068.750  25633.333   7248.500  66900.000  62812.500  67125.000
## [151]  88250.000  28300.000  78900.000  71093.750   9750.000  14085.714
## [157]  12350.000  15216.667  25670.000  26750.000  57414.286  21920.000
## [163]  43500.000  16912.500  19062.500  15666.667  65044.444  20583.333
## [169]  11358.333  34816.667  34750.000  39360.000  29092.857  24422.222
## [175]  23360.000  42685.714  29080.000  16983.333  21666.667  31960.000
## [181]  24400.000   7242.857  16180.000  28216.667   9633.333  32742.857
## [187]  28833.333  21360.000  29391.667  24414.286  34720.000  14083.333
## [193]  14860.000  17916.667  23133.333  27850.000  18370.000  16975.000
## [199]  45980.000  36700.000  33583.333  29750.000  35416.667  28614.286
## [205]  22000.000

We need standardized values for both the lag variable and the sale price variable to build the Moran’I scatterplot. Standardized values are just z scores for each observation($z_i =\frac{ x_i -\mu}{\sqrt{Var(x)}}$). To get the standardized values, we will use standardize from the robustHD package. We could very easily calculate these with Base R vectorized operations, but it is faster to just use a package function.

clev.points$standardized_sale_price <- standardize(clev.points$sale_price)
clev.points$standardized_lag_sale_price <- standardize(clev.points$lagged_sale_price)

To construct the moran’s I scatterplot, we will use ggplot2 for more aesthically pleasing plots. We will not go into too much depth on the options available for for these plots, but for more information, check out ggplot2 documentation. In addition, The first Exploratory Data Analysis notebook is also a good resource to look at.

To make the Moran’s I scatterplot, we make a scatterplot in ggplot2 with the standardized sale price values as the x axis and the standardized lag sale price variable as the y axis. We use geom_point to add the points to the plot. geom_smooth adds a regression line. The default option is a loess smooth line, we specify the method = lm to get a standard linear regression line . We add dotted lines at the x and y axis to separate the 4 types of spatial autocorrelation. We do this with geom_hline for the x axis and geom_vline for the y axis. To get the speciifcations of the scatterplot to better match up with GeoDa, we set the x and y scale limits to -10 and 10.

ggplot(data = clev.points, aes(x=standardized_sale_price, y = standardized_lag_sale_price)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  geom_hline(yintercept = 0, lty = 2) +
  geom_vline(xintercept = 0, lty = 2) +
  xlim(-10,10) +
  ylim(-10,10) + 
  ggtitle("Moran scatter plot sale price")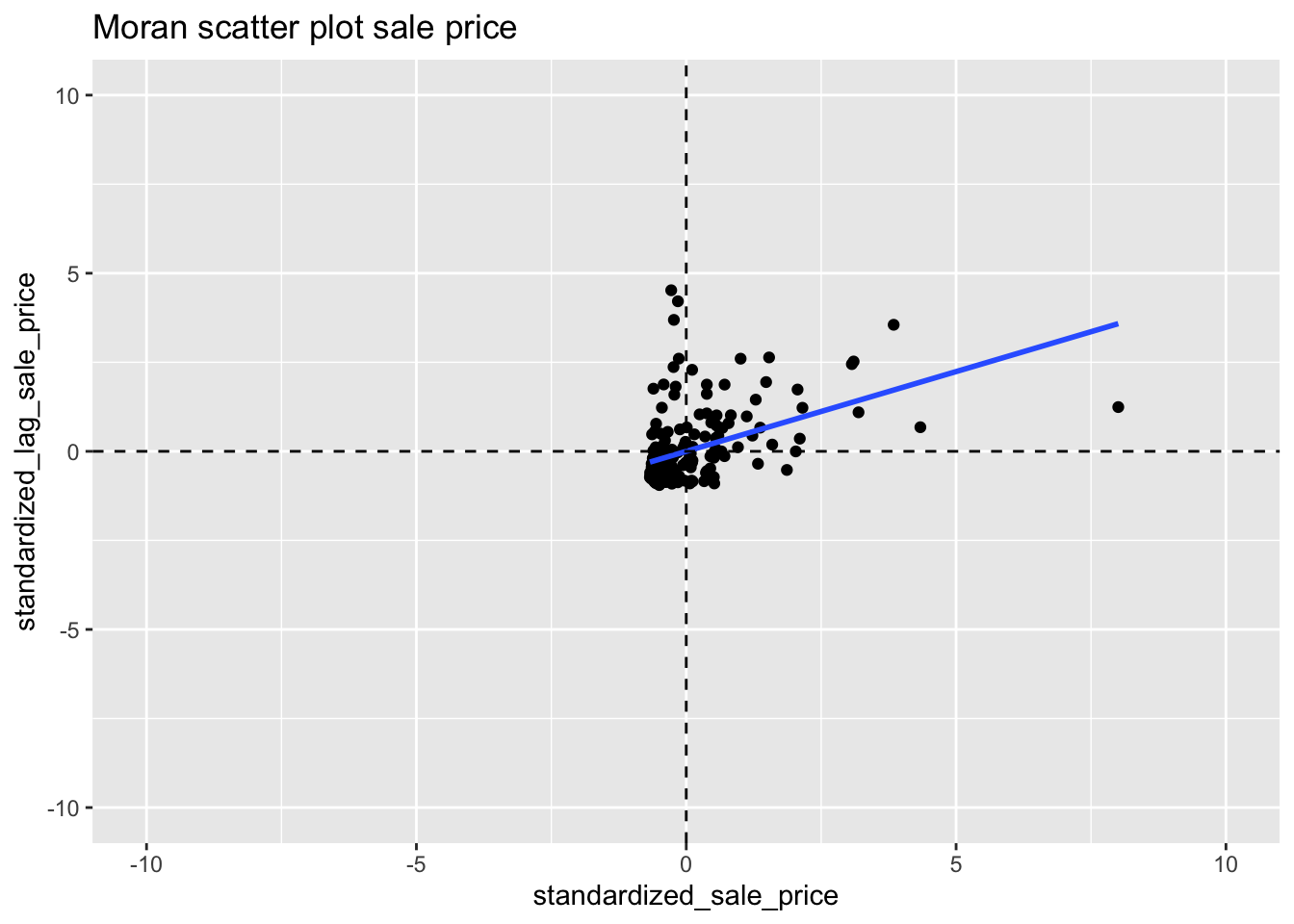

10.2.2.1 Interpretation

We can see that the shape of the point cloud is determined by the presence of several outliers on the high end (e.g., larger than three standard deviational units from the mean). One observation, with a sales price of 527,409 (compared to the median sales prices of 20,000), is as large as 8 standard deviational units above the mean. On the lower end of the spectrum (to the left of the dashed line in the middle that represents the mean), there is much less spread in the house prices, and those points end up bunched together. By eliminating some of the outliers, one may be able to see more detail for the remaining observations, but we will not pursue that here.

10.2.2.2 Assessing significance

We have an estimate of the Moran’s I statistic, but no information on the significance of that statistic. This can be obtained by constructing a distribution by means of random assignment. In order to do this, we first choose the number of permutations desired, which will directly affect the minimum pseudo p-value we can obtain for the test statistic. In the case of 999 permutation the minimum p-value would be .001, which would mean none of the sample distribution statistics are as extreme or more extreme than the test statistic.

10.2.2.2.1 Replicability - the random seed

To faciliate replication, it is best to set a seed for the random number generator. The one used in GeoDa is 123456789, so we will demonstrate how to set the seed here. It is just set.seed and the desired seed number as an input.

set.seed(123456789)

10.2.2.3 Reference distribution

To make the reference distribution, we will need to draw 999 randomized samples of the housing point data of the same size as the number of observations in the housing point data. This random sample will allow us to assign the values to random locations, which will give us a spatially random distribution. To get to this point, we will build up in steps in order to better understand the process.

We start by taking one random sample of our points with the base R sample function. We choose the same size as the number of sale price data observations to make a spatially randomized vector of our sale price data. The point of this is to randomly assign the housing prices to the voronoi polygons, then to compute the Moran’s I statistic for the spatially random assignment based off the original weights structure.

draw <- sample(clev.points$sale_price, size = length(clev.points$sale_price))
draw

##   [1]  28000  82500  14500 135000  29150  13000  25250  34750  30000  14000
##  [11]   3500  45000  76000   8000  25000  14500  15000   7500   5000  26400
##  [21]  40000  65000  25750  15000   5800   4924   9000  41000  65000 527409
##  [31]  29900   5968  11000  33500   6800  64000  41500  21199   8000  15000
##  [41]  47000   7900   8400   8000  16000  20000   9000  15500   4149  17500
##  [51]  22000  19000  27600  72900   5200   4775   4500   9500  32500   5000
##  [61] 122500   7000  26000   2910 138500 165000   2500  92000  15000  40000
##  [71]  75000  32500   5000   7000  11750  20000  49000  41069  49000  15000
##  [81]   6370  15000  26000  38200  15000  85000  62000 120000  65000  70000
##  [91]  25000  84900  65000  28500   1300   6483 155000  73400  13000   4000
## [101] 305000 230000  11750 100000  15000  21119  75000  42000  20000   3000
## [111]  76000  12000  20000  11500   5000  10000  25750 116250  13100   7000
## [121]  48000  16000  10000   1448  29000 167000   5000  25000   8500   6300
## [131]   8600  27750 235500  81500  78000 228000  69000   3000  32500  20000
## [141]   4250 169500  10000  10000   8000 109900  20000  19000   7000  56900
## [151]  47000 103000   1049   5500  10500  26000  25000 125000  23000  24900
## [161]  48500  13000  16500   5500  17000  11500  10000  12000  45900  51000
## [171] 131650  24800  11582   6375  73000  11750  16900 172500   7000   2100
## [181]  48500  16500  15000  42500 275000  18000  15834  89500   6500  27000
## [191]   8000  23500   5000  48900   5000  19971  63000  10000  72000  38500
## [201]   7000  12000  68900  34000   5000

Now we can begin to calculate the Moran’s I statistic by first calculating the spatial lag variable based on our queen weights and the spatially random sample.

lag1 <- lag.listw(queen.weights,draw)

We can get the Moran’s I statistic by regressing the standardized values of the spatial lag variable on the standardized values of the random draw. We can get the standardized value with the standardize function. The summary function allows us to see a summary of the regression statistics.

lmfit <- lm(standardize(lag1) ~ standardize(draw))
summary(lmfit)

## 
## Call:
## lm(formula = standardize(lag1) ~ standardize(draw))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.2872 -0.6826 -0.2114  0.3316  4.4708 
## 
## Coefficients:
##                     Estimate Std. Error t value Pr(>|t|)
## (Intercept)       -1.236e-16  6.997e-02   0.000    1.000
## standardize(draw)  3.735e-02  7.014e-02   0.532    0.595
## 
## Residual standard error: 1.002 on 203 degrees of freedom
## Multiple R-squared:  0.001395,   Adjusted R-squared:  -0.003525 
## F-statistic: 0.2835 on 1 and 203 DF,  p-value: 0.595

The slope here is the estimate for standardize(draw). This value is fairly close to zero as the randomization process makes makes the draw spatially random.

To build our distribution, we will need to repeat this process many times over. We can accomplish this by way of a for loop. We will need somewhere to store our Moran’s I result for each iteration. To do this we will make an empty vector of a length corresponding to our desired number of permutations.

randomized_moran <- rep(NA, 999)

The process here is the same as the one followed for one draw, but here we use the for loop to get 999 iterations and store the resulting Moran’s I values in the vector that we created above. First we do the random sample with the sample function. Then we make a lag variable based upon the random draw and our queen weights. Next we run the regression with the lm function between the stanardized values of the lag variable and random draw variable. Lastly, we extract the slope coefficient which is our Moran’s I statistic and store it in index i. Each iteration of the loop will store the value at the subsequent index ie 1, then 2, then 3, and so on.

for(i in 1:999){
  draw <- sample(clev.points$sale_price, size = length(clev.points$sale_price))
  lag <- lag.listw(queen.weights,draw)
  lmfit <- lm(standardize(lag) ~ standardize(draw))
  randomized_moran[i] <- lmfit$coefficients[2] 
}

We can obtain summary statistics of our distribution with summary

summary(randomized_moran)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -0.26210 -0.08531 -0.02554 -0.01655  0.04257  0.31351

sd(randomized_moran)

## [1] 0.09375454

Now to get the p value, we will check the number of samples that had higher Moran’s I statistic than the observed value. To do this, we use the base R which function to get a vector of the indices at which the conditional is TRUE. We then get the length of the vector with length.

length(which(randomized_moran > .281))

## [1] 4

Since the result is 1, there is only 1 value in all of the permutations that is higher than the test statistic. This means that the p value is .002, $\frac{1 + R}{1 + M}$, where R = 1 and M = 999.

There are a number of ways we can visualize the distribution that we just constructed in R. We will use ggplot2 to do these visualizations because it looks much better than base R visualizations.

To start, we convert our vector with the randomized moran’s I values into a data frame, so we can use ggplot2 functions. For this, we just use the data.frame function with the vector of randomized moran’s I values as an argument and then assign a name for the column, which is just moran in this case.

The first option is a density plot. This requires the standard ggplot function with aes containing the x axis. Additionally we need geom_density. We use geom_vline to plot the mean of the distribution and our observed statistic.

df <- data.frame(moran = randomized_moran)
ggplot(data = df,aes(x=moran)) +
  geom_density() +
  geom_vline(xintercept = moran[[1]], col = "green") +
  geom_vline(xintercept = mean(randomized_moran), col = "blue")

The next option is a histogram. The only difference here is that we use geom_histogram instead of `geom_density.

ggplot(data = df, aes(x=moran)) +
  geom_histogram() +
  geom_vline(xintercept = moran[[1]], col = "green") +
  geom_vline(xintercept = mean(randomized_moran), col = "blue")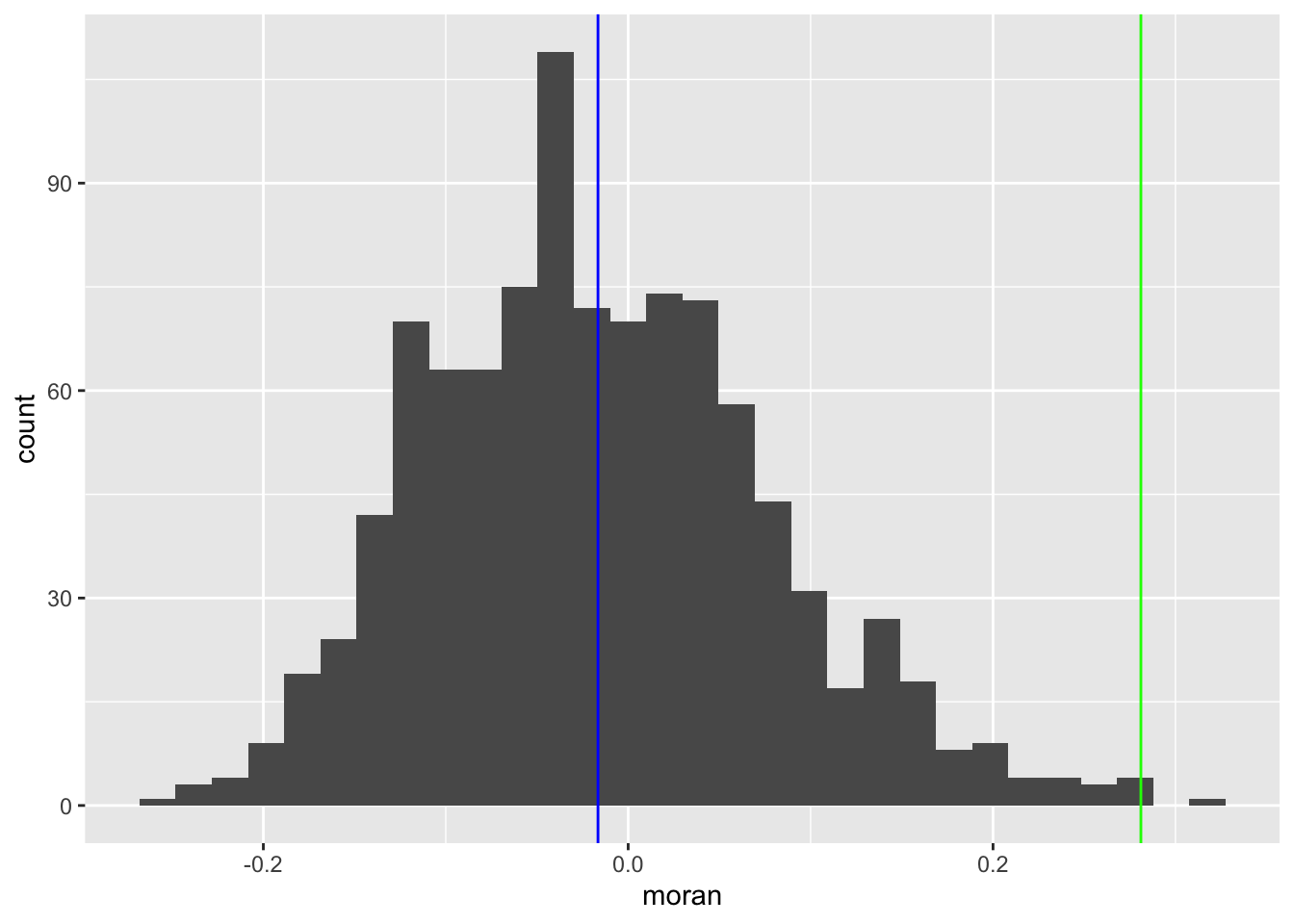

#### LOWESS smoother

The LOWESS smoother is not implemented directly in ggplot2, but can be found in an add-on package. We use the Hmisc package to add this functionality to the ggplot2 plots. To add the smoother to our Moran’s I scatter plot, we use the stat_plsmo from the Hmisc package. The default span for GeoDa is .2 so we will set the span = parameter to .2.

With the LOWESS smoother, we can see potential structural breaks in the pattern of spatial autocorrelation. For example some parts of the data, the curve may be very steep, and positive, indicating strong spatial autocorrelation, whereas in other parts, it could be flat, indicating no spatial autocorrelation.

ggplot(data = clev.points, aes(x=standardized_sale_price, y = standardized_lag_sale_price)) +
  geom_point() +
  stat_plsmo(span = .2, color = "blue") +
  geom_hline(yintercept = 0, lty = 2) +
  geom_vline(xintercept = 0, lty = 2) +
  xlim(-10,10) +
  ylim(-10,10) + 
  ggtitle("LOWESS smooth of Moran Scatterplot")

10.2.2.4 Chow test Moran’s I scatterplot

The Chow test is a statistical test of whether or not the coeffiecients of two different linear regressions are equal. In the case of the Moran’s I scatterplot, it is just the slope of the regression line and the intercepts, since it is a simple linear regression.

The brushing operation in GeoDa is fairly difficult to implement in R, but we can do a less interactive version. First we must consider which criteria we want to select points on. This could be anything from its location to other characteristics in the data. In our case we will do it based on location. As an approximation for the midpoint of the set of points, we take the the mean of the x and y coordinates. From there we assign “Select” to the points in the bottom left quadrant and “Rest” to the rest of the points by way of the if_else function. This function takes a conditional, a result to assign in the case where the conditional is TRUE, and a result to assign when the conditional is FALSE. In our case it is “Select” and “Rest”.

mid_x <- mean(clev.points$x)
mid_y <- mean(clev.points$y)
clev.points<- clev.points %>% mutate(bottom_left = if_else((x < mid_x & y < mid_y),"Select", "Rest"))

Before we run the chow test, we will visualize the difference in slopes of the selected data, non-selected data and the aggregate data. With ggplot2, we can accomplish this by setting categorical colors based whether or not an observation is “Selected” or “Rest”. To do this, we specify aes(color = bottom_left) in both geom_point and geom_smooth. This will give us colored points and regression lines for “Selected” and “Rest”. Then to get blue and red colors, we use scale_color_manual. For this plot, we do not set x and y limits because the -10 to 10 speciifcation is too dificult to see the differences in the regression lines.

ggplot(clev.points, aes(x=standardized_sale_price,y=standardized_lag_sale_price)) +
  geom_point(aes(color=bottom_left)) +
  geom_smooth(aes(color=bottom_left), method = lm, se = FALSE) +
  geom_smooth(method=lm,se = FALSE, color = "black") +
  scale_color_manual(values=c("blue","red"))  +
  labs(color="Selection") +
  geom_hline(yintercept = 0, lty = 2) +
  geom_vline(xintercept = 0, lty = 2) +
  ggtitle("Chow test Moran Scatterplot")

To perform the chow test, we need two separate data frames as inputs for the function. To get the two data frames, we use the tidyverse filter function. This function filter out observations based on a conditional. TRUE values for the conditional remain in the data frame while FALSE values are filtered out.

clev.select <- clev.points %>% filter(bottom_left == "Select")
clev.rest <- clev.points %>% filter(bottom_left == "Rest")

Now we use the base R lm function to run separate regressions on the standardized lag variable and standardized sale price variable.

reg.select <- lm(standardized_lag_sale_price~standardized_sale_price, data=clev.select)
reg.rest <- lm(standardized_lag_sale_price~standardized_sale_price, data=clev.rest)

Now we use the summary function on each regression object to get summary statistics of the residuals, the regression coefficients and and their respective standard errors, the R squared values, and the F statistic.

summary(reg.select)

## 
## Call:
## lm(formula = standardized_lag_sale_price ~ standardized_sale_price, 
##     data = clev.select)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.32083 -0.26382 -0.08486  0.25641  2.38954 
## 
## Coefficients:
##                         Estimate Std. Error t value Pr(>|t|)    
## (Intercept)             -0.15667    0.06062  -2.584   0.0117 *  
## standardized_sale_price  0.51228    0.11818   4.335 4.53e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.492 on 74 degrees of freedom
## Multiple R-squared:  0.2025, Adjusted R-squared:  0.1917 
## F-statistic: 18.79 on 1 and 74 DF,  p-value: 4.534e-05

summary(reg.rest)

## 
## Call:
## lm(formula = standardized_lag_sale_price ~ standardized_sale_price, 
##     data = clev.rest)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.2276 -0.6161 -0.3336  0.2146  4.5370 
## 
## Coefficients:
##                         Estimate Std. Error t value Pr(>|t|)    
## (Intercept)              0.10241    0.09335   1.097    0.275    
## standardized_sale_price  0.42072    0.07816   5.383 3.42e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.056 on 127 degrees of freedom
## Multiple R-squared:  0.1858, Adjusted R-squared:  0.1793 
## F-statistic: 28.97 on 1 and 127 DF,  p-value: 3.418e-07

We see that the slopes vary by about .08 and the intercepts vary by .25

To run the chow test, we need 4 inputs for chow.test. We need the two standardized variables from the the “Select” data frame: clev.select and the two standardized variables from the the “Rest” data frame: clev.rest.

chow <- chow.test(clev.select$standardized_lag_sale_price, clev.select$standardized_sale_price, clev.rest$standardized_lag_sale_price, clev.rest$standardized_sale_price)
chow

##     F value       d.f.1       d.f.2     P value 
##   2.2974700   2.0000000 201.0000000   0.1031467

With a p-value of .103 we do not have significant evidence to conclude that the slopes of the two regressions are different under a standard alpha level of .05.

10.3 Spatial Correlogram

10.3.1 Concept

A non-parametric spatial correlogram is an alternative measure of global spatial autocorrelation that does not rely on the specification of a spatial weights matrix. Instead, a local regression is fit to the covariances or correlations computed for all pairs of observations as a function of the distance between them (for example, as outlined in Bjornstad and Falck 2001).

With standardized variables z, this boils down to a local regression:

\[z_iz_j = f(d_{ij}) + u\]

where $d_{ij}$ is the distance between a pair of locations i - j, u is an error term and f is a non-parametric function to be determined from the data. Typically, the latter is a LOWESS or kernel regression.

10.3.2 Creating a spatial correlogram

In GeoDa, creating a spatial correlogram is much more straight forward than in R. The process in r requires us to start with the sale price points, then to create a neighbors structure base on the distance breaks desired for the correlogram.

To start, we use cbind to put the x and y coordinates together for use in the distance based neighbor functions of spdep.

coords <- cbind(clev.points$x, clev.points$y)

Now we create distance based neighbors coordinate matrix and lower distance bound and an upper distance bound, which is used to define neighbors. We use dnearneigh to create the distance band neighbors. For more in depth information on distance based neighbors, please see the Disatnce Based Weights notebook. We use a distance of 4823.27 to emulate the first example in the GeoDa workbook.

dist.band.nb <- dnearneigh(coords,0,4823.27)

Using the spdep function `sp.correlogram, we can get measures of spatial autocorrelation for an input number of lag orders. We can then use the base R plotting function to get a look at the autocorrelation values for each lag order.

sp <- sp.correlogram(dist.band.nb, clev.points$sale_price, order = 10, method = "I",style = "W", randomisation = TRUE, spChk = NULL, zero.policy = TRUE)
plot(sp)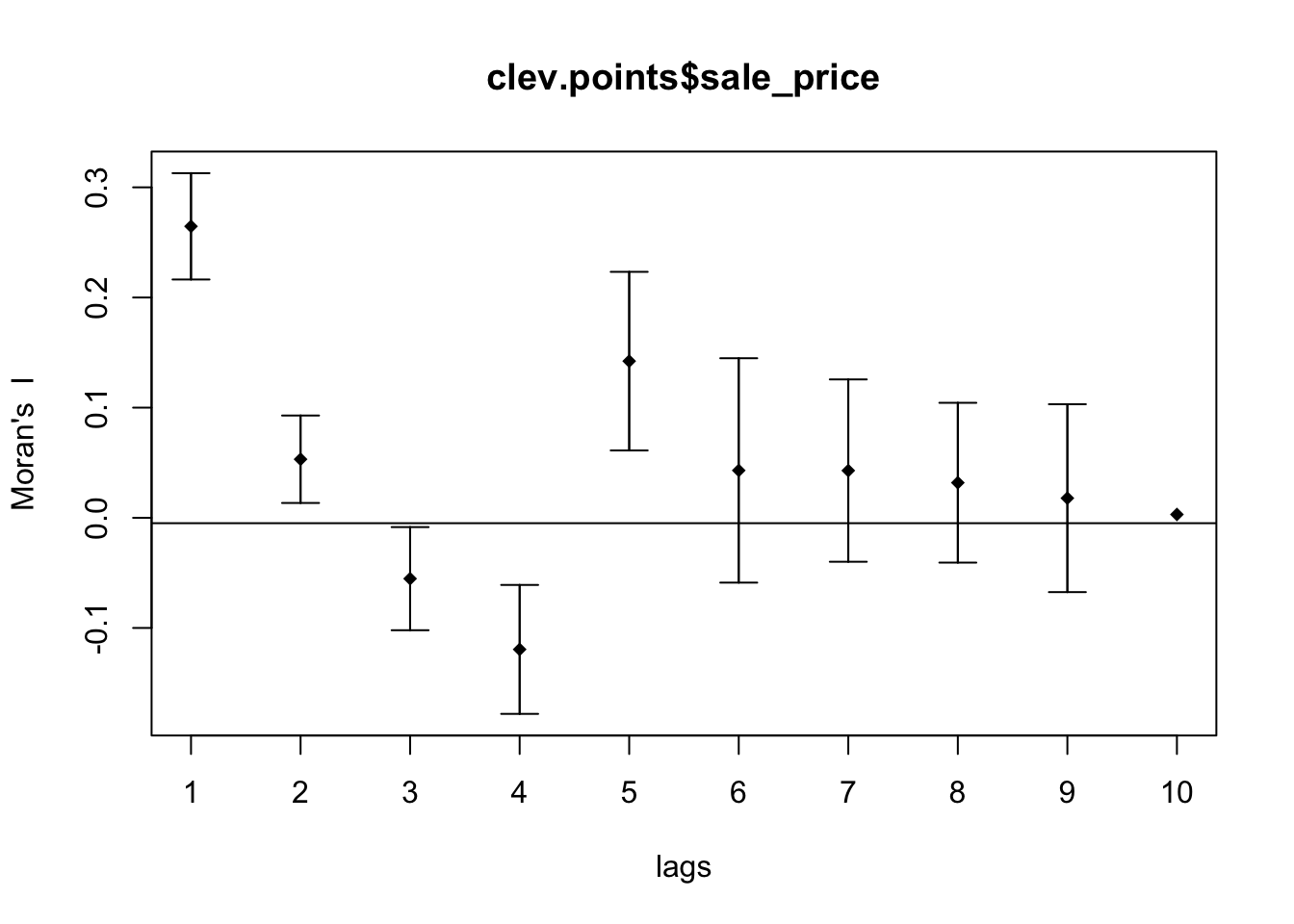

To get a better looking plot, we can extract the moran’s I values and put them into a data frame, so we can use ggplot2 plotting functionality.

morans <- sp$res[,1]
df <- data.frame(Morans_I = morans,lags = 1:10 )
ggplot(data = df, aes(x=lags,y=Morans_I)) +
  geom_point() +
  geom_smooth(col = "purple", se = FALSE) +
  geom_hline(yintercept = 0) +
  ylim(-.5,.5)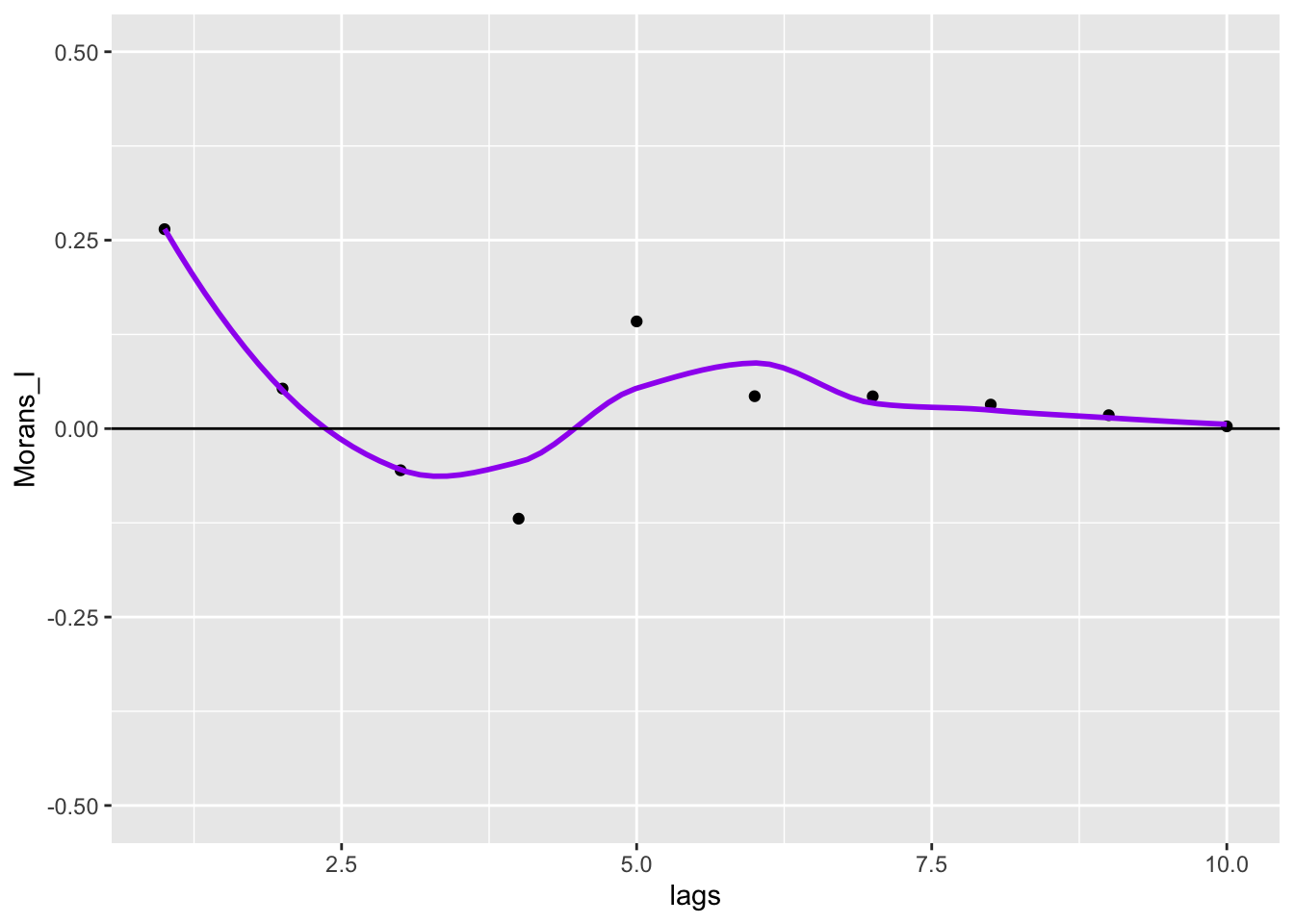

To get closer to the GeoDa correlogram plotting functionality, we can convert lags to euclidean distance.

df$euclidean_distance <- df$lags * 4823.3
ggplot(data = df, aes(x=euclidean_distance,y=Morans_I)) +
  geom_point() +
  geom_smooth(col = "purple", se = FALSE) +
  geom_hline(yintercept = 0) +
  ylim(-.5,.5) +
  scale_x_continuous(breaks = df$euclidean_distance)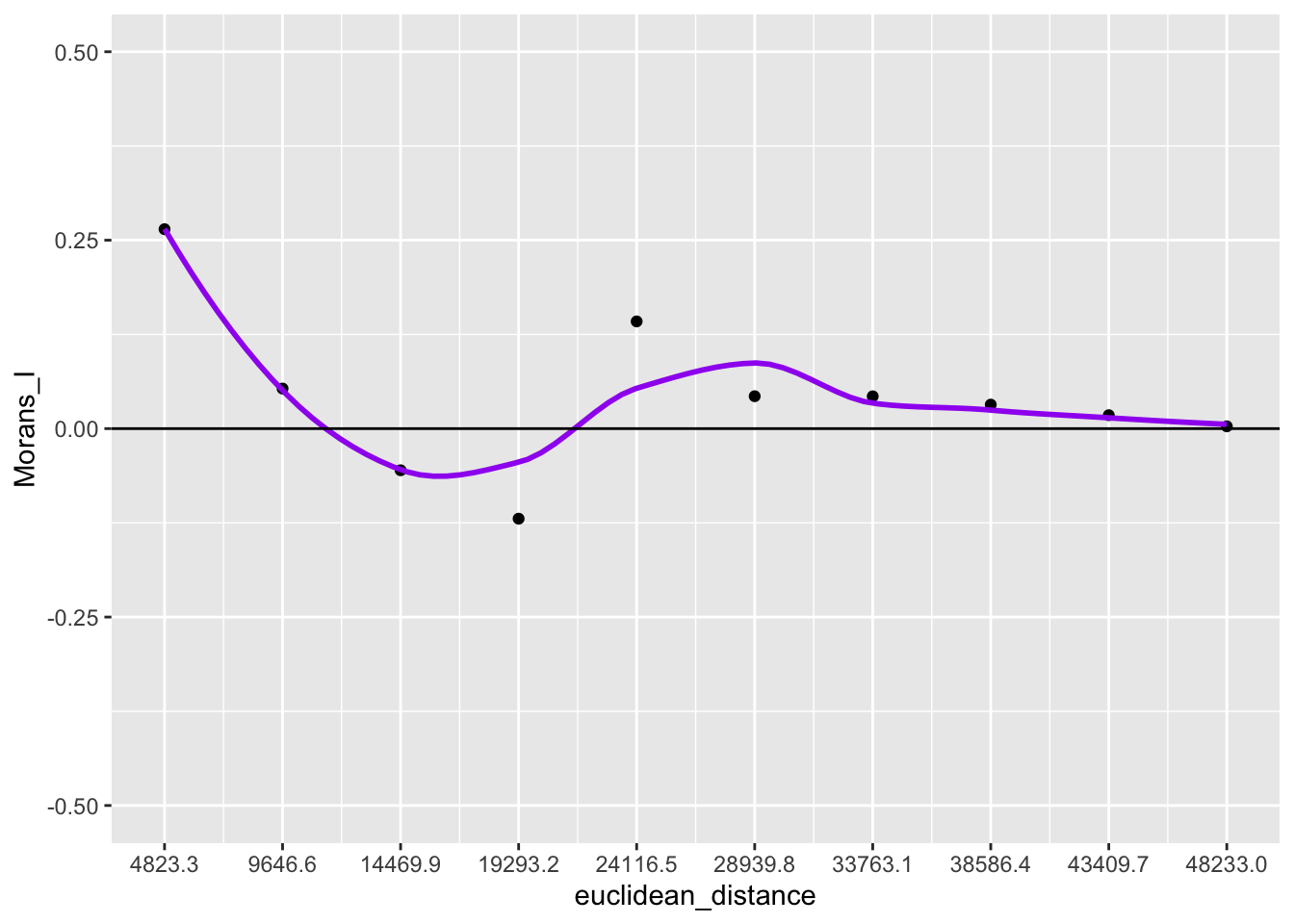

The spatial correlogram can be paired with a bar chart that shows the number of neighbor pairs for each lag order. To get this information, we will need to work outside the spdep package and compute them ourselves.

To begin, we set up an empty vector to store the pair numbers.

pairs <- rep(NA, 10)

Here we run dnearneigh on each interval of euclidean distance that corresponds to a lag in 1 to 10. To get the number of pairs for each lag order, we simply sum up the cardinality of the neighbor structure per each lag order and then divide it by two because this sum gives the total number of neighbors and the total number of pairs will be half this number.

for (i in 1:10){
  nb <- dnearneigh(coords, (i - 1) * 4823.28, i * 4823.28)
  pairs[i] <- sum(card(nb)) / 2
}

Now we create a data frame from the two vectors we create with the lag order values and associated euclidean distance values.

df <- data.frame(lag_order = 1:10, auto_corr = morans, num_pairs = pairs)
df$euclidean_distance <- df$lag_order * 4823

Here we create two different plots, one is a histogram with the number of pairs in each bin, the other is the spatial correlogram

p1 <- ggplot(data = df, aes(x = euclidean_distance,y = auto_corr)) +
    geom_point() +
    geom_smooth(col = "purple", se = FALSE) +
    geom_hline(yintercept = 0) +
    ylim(-1,1) +
  scale_x_continuous(breaks = df$euclidean_distance)
p2 <- ggplot(data = df, aes(x=euclidean_distance,y = num_pairs, fill = as.factor(euclidean_distance))) +
  geom_bar(stat = "identity") +
  scale_fill_brewer(palette = "Paired") +
  theme(legend.position = "none") +
  geom_text(aes(label=num_pairs), position = position_dodge(width = .9), vjust=-.25) +
  ylim(0, 1.2 * max(pairs)) +
  scale_x_continuous(breaks = df$euclidean_distance)
p1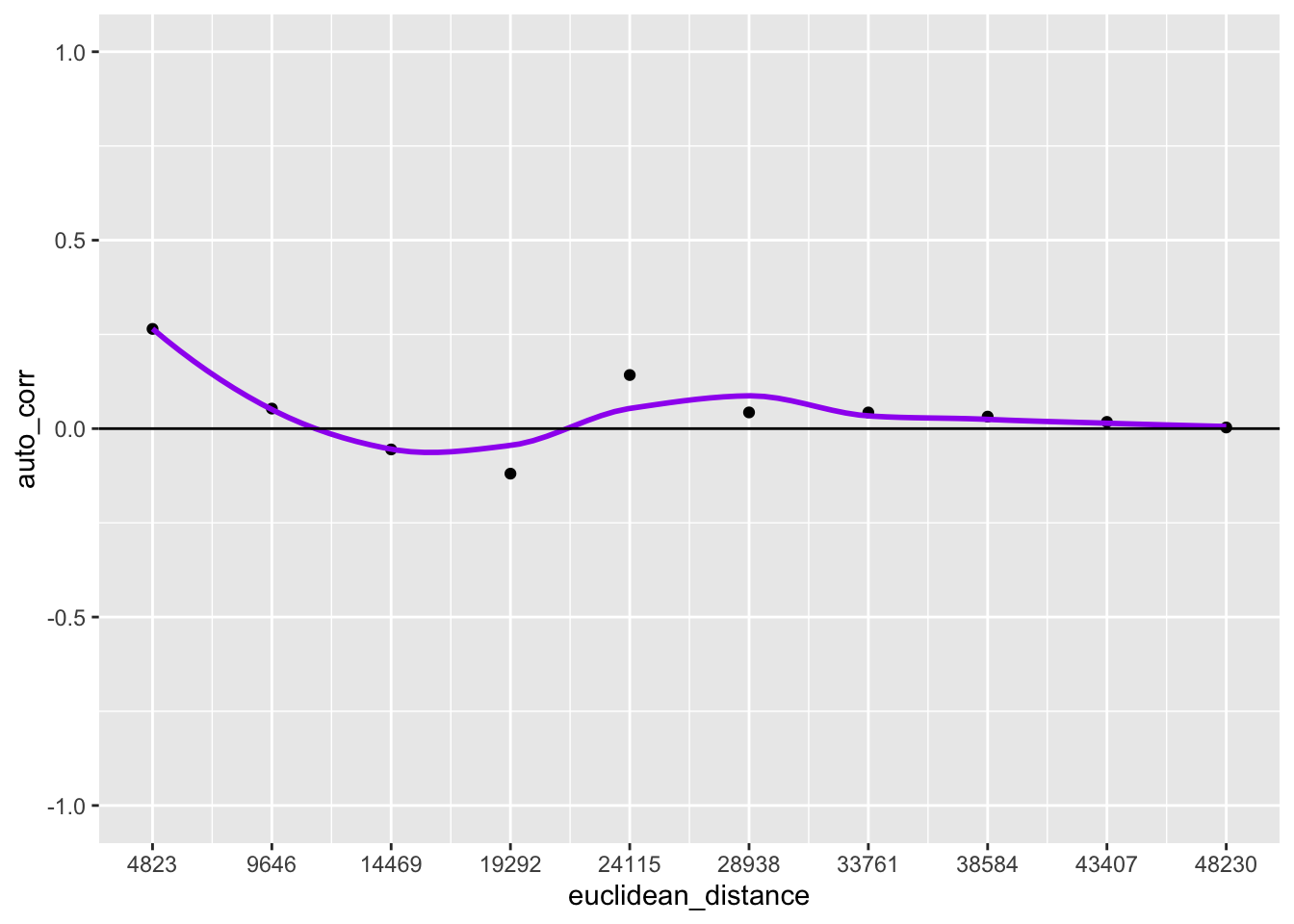

p2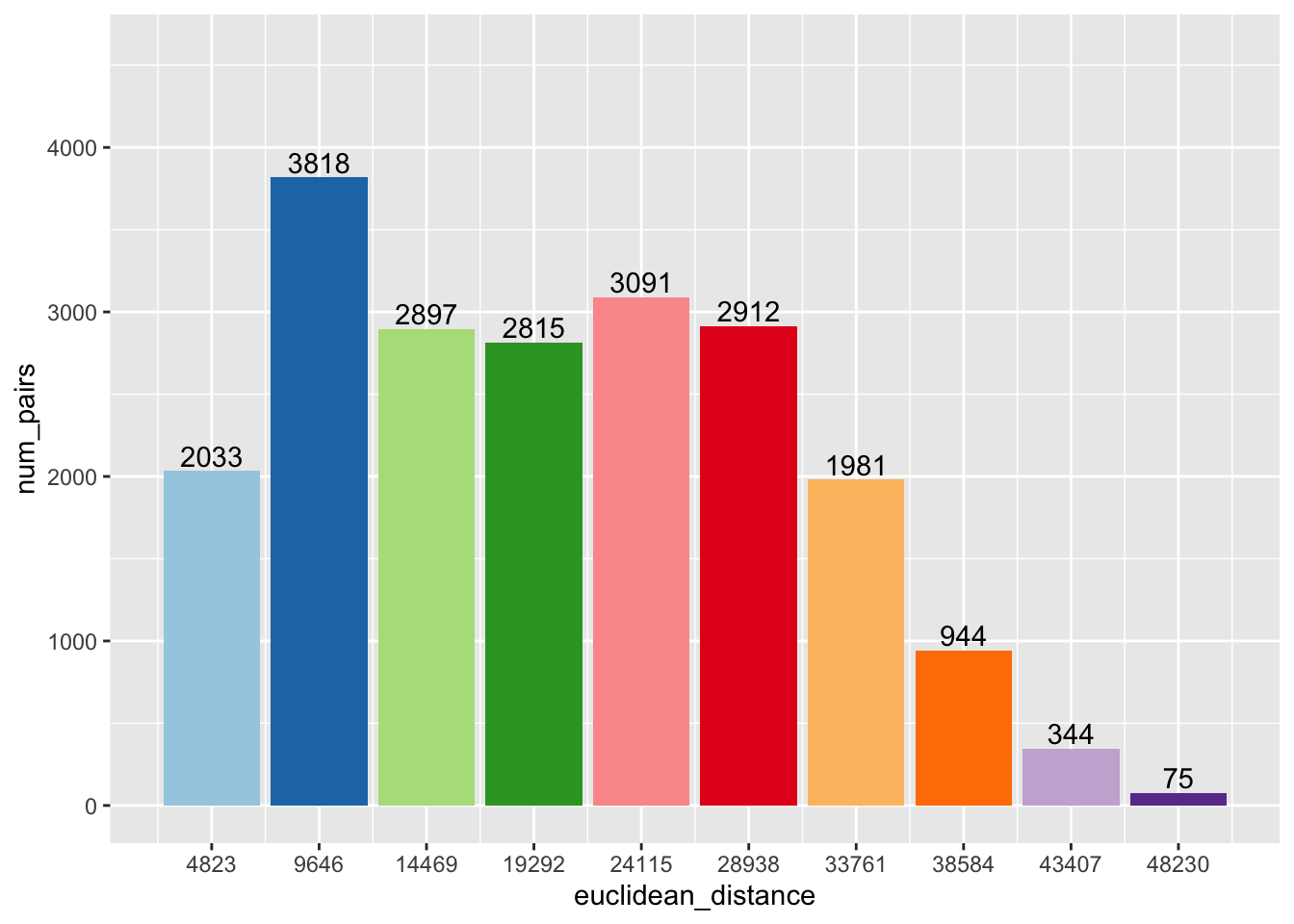

Using grid.arrange from the gridExtra package, we can combine the two plots into one image.

grid.arrange(p1,p2,ncol = 1)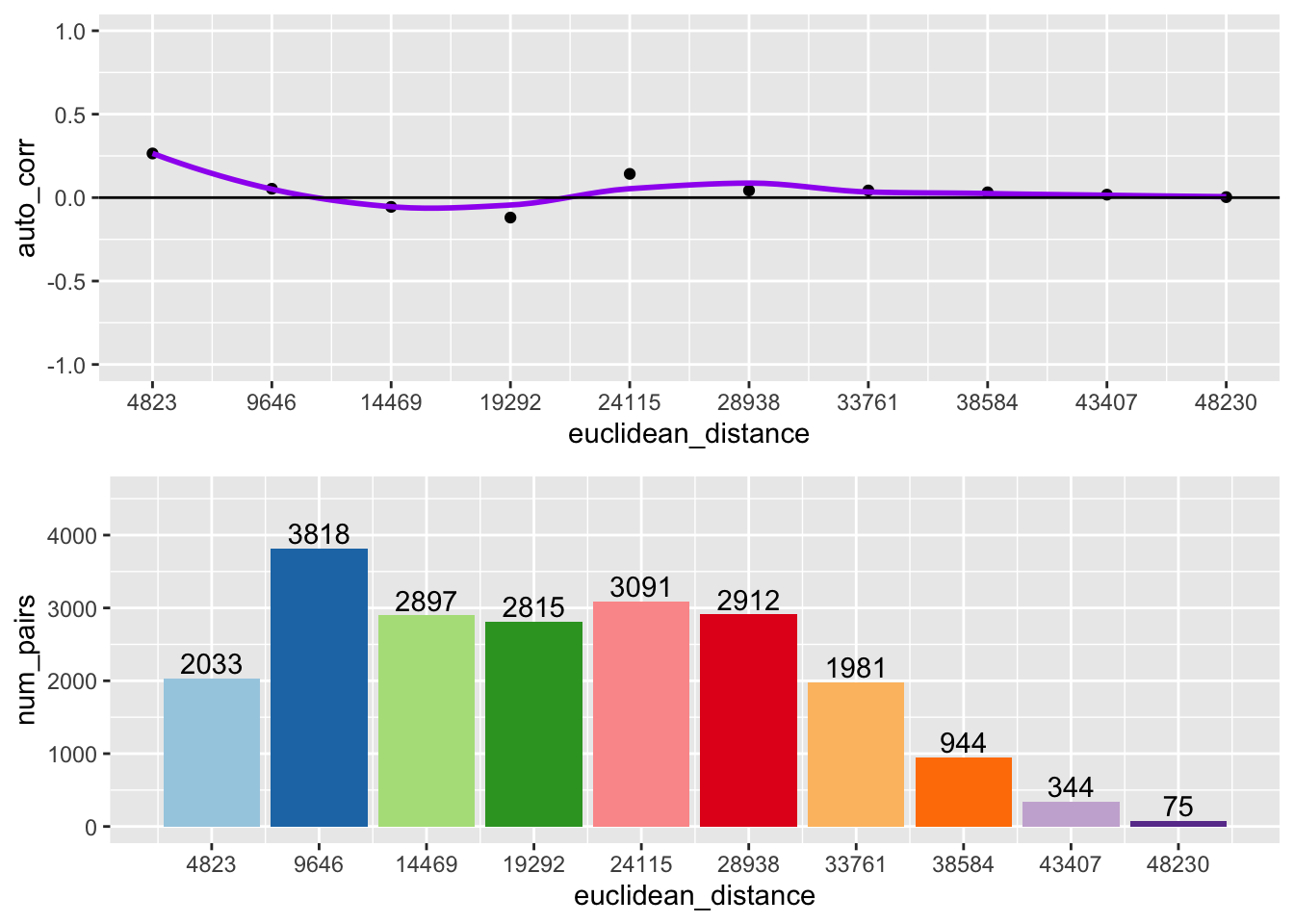

Following the same process outlined above, we can make a function that constructs the correlogram based on the desired lag order, distance band, variable, and coordinates.

geoda_correlogram <- function(lag.order, distance, var,coords){
  # Funtion that outputs a spatial correlogram with a bar plot of neighbor pairs
  # Inputs:
  #        lag.order: The desired number of lag orders to be included in the plot
  #        distance: The desired distance band for the lags
  #        var: A variable to analyze the spatial autocorelation
  #        coords: A matrix of coordinates of the same length as var
  # creating vectors to store autocorrelation values and number of pairs
  pairs <- rep(NA, lag.order)

  #loop to calculate number of pairs for each lag order
  for(i in 1:lag.order) {
    nb <- dnearneigh(coords, (i-1) * distance, i * distance)
    pairs[i] <- sum(card(nb)) / 2
  }
  
  # Computing spatial autocorrelation
  nb1 <- dnearneigh(coords, 0 , distance)
  sp <- sp.correlogram(nb1, var, order = lag.order, method = "I", style = "W", randomisation = FALSE, spChk = NULL, zero.policy = TRUE)
  
  # Putting the lag orders, autocorrelation, pairs and distance into a dataframe
  df <- data.frame(lag = 1:lag.order, num_pairs = pairs, auto_corr = sp$res[,1])
  df$euclidean_distance <- df$lag * round(distance, digits = 0)
  
  # Making plots
  p1 <- ggplot(data = df, aes(x = euclidean_distance,y = auto_corr)) +
    geom_point() +
    geom_smooth(col = "purple", se = FALSE) +
    geom_hline(yintercept = 0) +
    ylim(-1,1)  +
    scale_x_continuous(breaks = df$euclidean_distance)
  p2 <- ggplot(data = df, aes(x=euclidean_distance,y=num_pairs, fill = as.factor(euclidean_distance))) +
    geom_bar(stat= "identity") +
    scale_fill_brewer(palette = "Paired") +
    theme(legend.position = "none") +
    geom_text(aes(label=num_pairs), position = position_dodge(width = .9), vjust=-.25) +
    ylim(0, 1.2 * max(pairs)) +
    scale_x_continuous(breaks = df$euclidean_distance)
  grid.arrange(p1,p2,ncol =1)
}
geoda_correlogram(10, 4823.3, clev.points$sale_price, coords)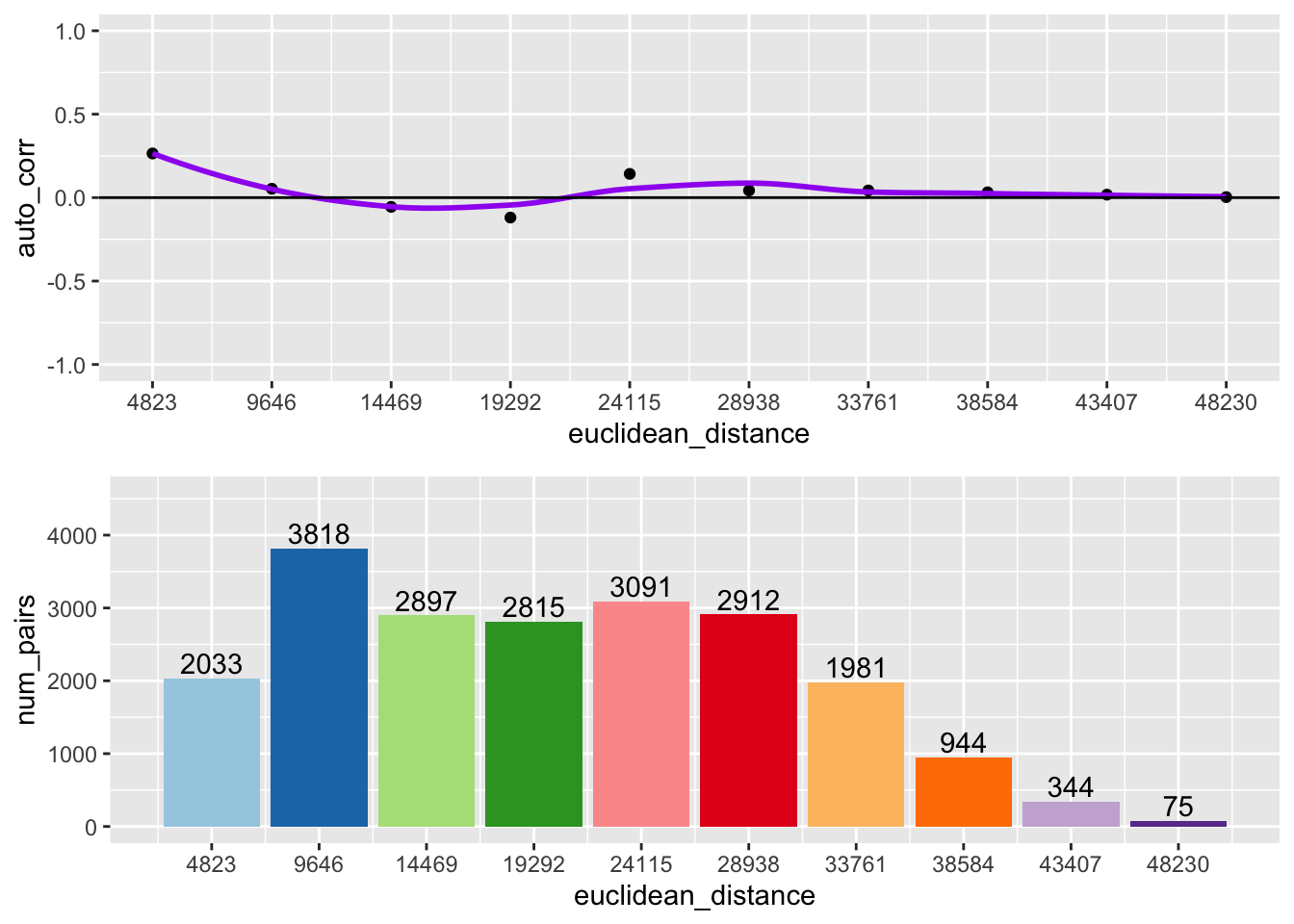

10.3.3 Interpretation

The top of the above graph is the actual correlogram. This depicts how spatial autocorrelation changes with distance. The first dot correpsonds with distances between 0 and 4823 feet. The dashed line indicates a spatial autocorrelation of 0. The autocorrelation starts positive and then fluctates above and below the dashed line.

Use setwd(directorypath) to specify the working directory.↩︎
Use install.packages(packagename).↩︎